
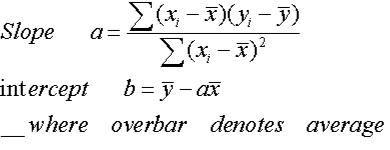
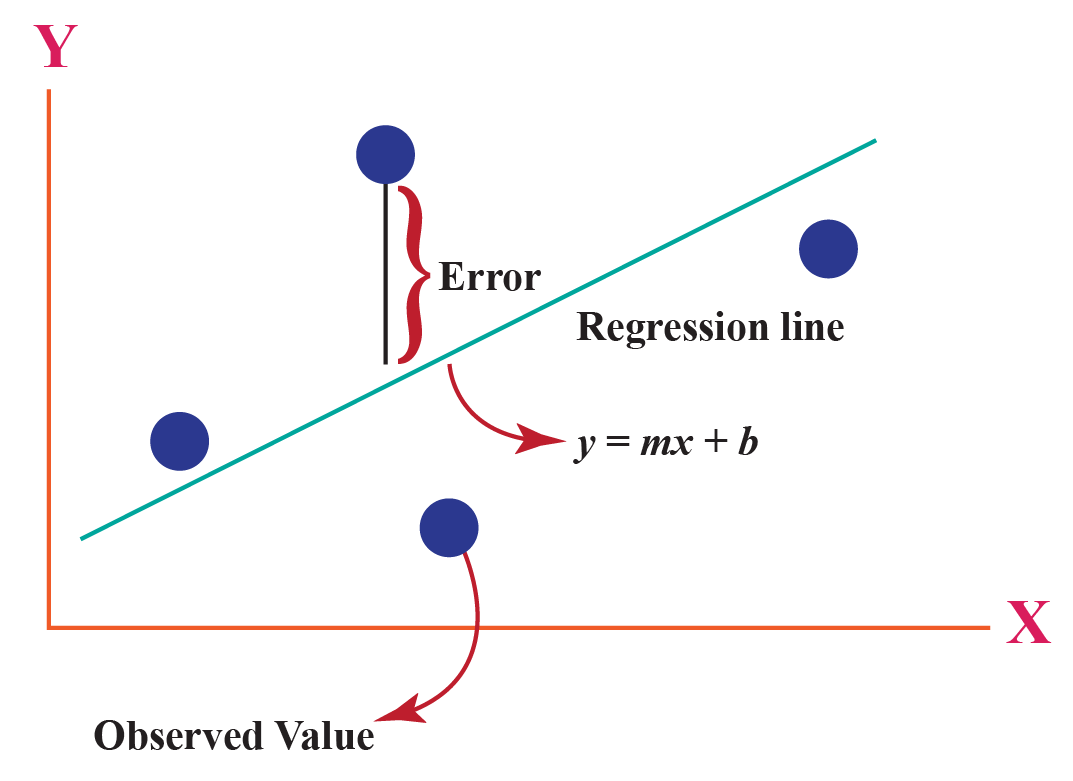
If the observed data point lies below the line, the residual is negative and the line overestimates that actual data value for y. If the observed data point lies above the line, the residual is positive and the line underestimates the actual data value for y. In other words, it measures the vertical distance between the actual data point and the predicted point on the line, or it measures how far the estimate is from the actual data value. The absolute value of a residual measures the vertical distance between the actual value of y and the estimated value of y. It is not an error in the sense of a mistake. The term y 0 – ŷ 0 = ε 0 is called the error or residual.

It is not generally equal to y from data, but it is still important because it can help make predictions for other values. It is the value of y obtained using the regression line. The ŷ is read y hat and is the estimated value of y. Each point of data is of the the form ( x, y), and each point of the line of best fit using least-squares linear regression has the form ( x, ŷ). Rounding to the nearest tenth, the calculator gives the –median-median line of y = 6.9 x − 315.5.
#LEAST SQUARES REGRESSION LINE EQUATION CALCULATOR MANUAL#
The calculator shows a slight deviation from the previous manual calculation as a result of rounding. The slope, a, and y-intercept, b, will be provided. You can enter the x and y values into two separate lists choose Stat, Calc, Med-Med, and press Enter. The median–median line may also be found using your graphing calculator. Thus, the equation can be written as y = 6.9 x − 316.3. The line of best fit is represented as y = m x + b. Substituting these sums and the slope into the formula gives b = 476 − 6.9 ( 206.5 ) 3 b = 476 − 6.9 ( 206.5 ) 3, which simplifies to b ≈ − 316.3. The sum of the median x values is 206.5, and the sum of the median y values is 476. The y-intercept may be found using the formula b = Σ y − m Σ x 3 b = Σ y − m Σ x 3, which means the quantity of the sum of the median y values minus the slope times the sum of the median x values divided by three. Substituting the median x and y values from the first and third groups gives m = 174 − 143 71 − 66.5, m = 174 − 143 71 − 66.5, which simplifies to m ≈ 6.9. The slope can be calculated using the formula m − y 2 − y 1 x 2 − x 1. This allows us to find the slope and y-intercept of the –median-median line. When this is completed, we can write the ordered pairs for the median values. Table 12.3 shows the correct ordering of the x values but does not show a reordering of the y values. However, to find the median, we first must rearrange the y values in each group from the least value to the greatest value. The corresponding y values are then recorded. We must remember first to put the x values in ascending order. The first and third groups have the same number of x values. We first divide our scores into three groups of approximately equal numbers of x values per group. If multiple data points have the same y values, then they are listed in order from least to greatest y (see data values where x = 71).
Remember that this is the data from Example 12.5 after the ordered pairs have been listed by ordering x values. Let'’s first find the line of best fit for the relationship between the third exam score and the final exam score using the median-median line approach. We can obtain a line of best fit using either the median-–median line approach or by calculating the least-squares regression line. If each of you were to fit a line by eye, you would draw different lines. We will plot a regression line that best fits the data. The most basic linear equation is a first-degree equation with one variable, usually written in the form of y = mx + b, where m is the slope of the line and b is the y-intercept.The third exam score, x, is the independent variable, and the final exam score, y, is the dependent variable.What is the most basic linear equation?.Here are a few ways to identify a linear equation: Look at the degree of the equation, a linear equation is a first-degree equation.Ĭheck if the equation has two variables.There are four common methods to solve a system of linear equations: Graphing, Substitution, Elimination and Matrix.What are the 4 methods of solving linear equations?.The y-intercept is the point at which x=0. To find the slope use the formula m = (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are two points on the line. To find the linear equation you need to know the slope and the y-intercept of the line.It can be written in the form: y = mx + b where m is the slope of the line and b is the y-intercept. A linear equation represents a straight line on a coordinate plane.


 0 kommentar(er)
0 kommentar(er)
